#03 多変数解析
多変数関数
1変数関数は\(x\)に対して\(y\)を一意に対応付ける関係のことであった.この関係を\(y=f(x)\)等と書いた.
多変数関数は,\(n\)個の変数\(x_1,x_2,\cdots,x_n\)を\(y\)に対応づける関係のことであり, これを\(y=f(x_1,x_2,\cdots,x_n)\),または\(y=f(\boldsymbol{x})\)と書いたりする.
\[
\boldsymbol{x} = (x_1 x_2 \cdots x_n)^{\mathrm{T}} \longmapsto f(\boldsymbol{x})
\]
というようにベクトル\(\boldsymbol{x}\)と\(f(\boldsymbol{x})\)の対応付けとして見ることもできる. こちらの見方の方が後々微分等で直感的に理解しやすいという利点がある.
例1
多変数関数
\[
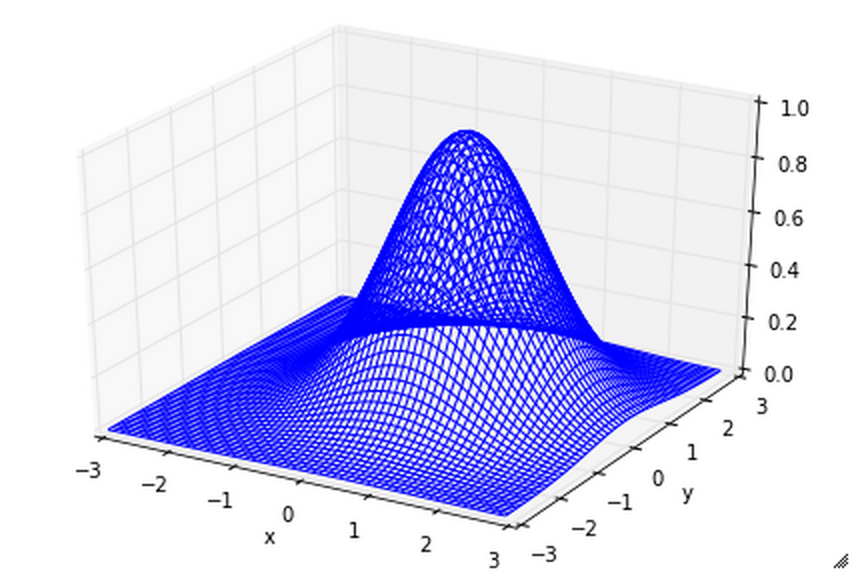
f(\boldsymbol{x}) = \exp\left(-\frac{(x-0.5)^2+(y-0.2)^2}{2}\right)
\]
をプロットする.matplotlibを用いると,以下のようなコードでプロットできる.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x, y = np.meshgrid(np.arange(-3,3,0.1), np.arange(-3,3,0.1))
z = np.exp(-((x-0.5)**2+(y-0.2)**2)/2)
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_wireframe(x,y,z)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
偏微分
1変数関数と同様に多変数関数でも微分を行うが,多変数関数では引数が複数個あるので,どの変数で微分するかで導関数が変化する.
関数\(f(x_1,\cdots,x_n)\)の引数のうち\(x_i\)以外を固定(定数と見なす)し,\(x_i\)で微分したときの導関数を
\[
\frac{\partial f}{\partial x_i}
\]
と書き,偏導関数という.
ベクトルによる微分
多変量解析では
\[
\frac{\partial(\boldsymbol{a}^{\mathrm{T}}\boldsymbol{x})}{\partial\boldsymbol{x}}
\]
のようにベクトルで微分を行う操作が式変形の過程で登場することがある. これは以下の略記である.
\begin{align}
\frac{\partial(\boldsymbol{a}^{\mathrm{T}}\boldsymbol{x})}{\partial\boldsymbol{x}}
&= \frac{\partial(a_1x_1+\cdots+a_nx_n)}{\partial \left(\begin{array}{c} x_1 \\ : \\ x_n \end{array}\right)} \\
&= \left(\begin{array}{c} \frac{\partial}{\partial x_1}(a_1x_1+\cdots+a_nx_n) \\ : \\ \frac{\partial}{\partial x_n}(a_1x_1+\cdots+a_nx_n) \end{array}\right) \\
&= \left(\begin{array}{c} a_1 \\ : \\ a_n \end{array}\right) \\
&= \boldsymbol{a}
\end{align}
このように,ベクトルで微分する場合も結果はスカラーの場合から連想される直感的な結果になる.
2次形式
\[
\boldsymbol{x}^{\mathrm{T}}\boldsymbol{Bx}=\sum_{i=1}^n\sum_{j=1}^n b_{ij}x_ix_j
\]
の微分も頻出なので,結果のみ示しておく.興味のある人は手を動かして計算してみるとよい.
\begin{align}
\frac{\partial\boldsymbol{x}^{\mathrm{T}}\boldsymbol{Bx}}{\partial\boldsymbol{x}}
&= (\boldsymbol{B}+\boldsymbol{B}^{\mathrm{T}})\boldsymbol{x} \\
&= 2\boldsymbol{Bx}^{\mathrm{T}} \; (\boldsymbol{B}:\mathrm{symmetric\,matrix})
\end{align}