確率は統計解析と密接に関係している． 例えば，株価のトレードデータから数日後の株価を予測する際，過去の統計データをもとに確率的に最もありえる株価でもって予測したりする． また，患者の状態を観測してそこから医者が”最も取るべき行動”を推論し，医療に応用するといったこともなされる．

本節では，確率解析のベースとなる確率分布の基礎を説明する．

二項分布

確率分布の最も単純な例として，コイン投げを考える． 確率\(p=\frac{1}{2}\)で表，\(q=1-p=\frac{1}{2}\)で裏が出るようなコインを考える． 確率変数\(x\)に対して「表が出る」事象を1，「裏が出る」事象を0とする． コインを\(n\)回投げるとき，表が出る回数が\(k\)回になる確率は以下のように表される．

\[ P(x=k) = {}_nC_k p^k(1-p)^{n-k} = \frac{n!}{k!(n-k)!} p^k(1-p)^{n-k} \]

（高校で学ぶ反復事象の確率そのものである）

このような確率変数\(x\)の分布はパラメータ\(n,p\)で決定されるため，二項分布\(B(n,p)\)に従うといい\(x\sim B(n,p)\)と書く．

二項分布をとるのは，試行がベルヌーイ試行（試行の結果が二値）であり，互いに独立であるような場合である． 上の例ではコイントスが試行であり，コイントス自体は表と裏の二値で，一回前のトスの結果は次のトスには影響しない．

例1

以下のスクリプトは二項分布に従って確率変数をランダムに生成している．

from scipy.stats import binom
print(binom.rvs(20, 0.5, size=10))

コイントスの例で言えば，「表裏が出る確率の等しい(p=0.5)コインを20回(=n)投げる」という試行を10回行っている． 実行例は以下のとおり．

array([12, 11,  9,  9,  7, 10, 10, 10,  9, 11])

このように，だいたい10回前後表が出ていることがわかる．

scipy.statsには他にも様々な確率分布に関するモジュールが提供されている． また，各々のモジュールは統一的なインターフェースで提供されている（例えば，他の確率分布に従って確率変数をランダム生成する場合もrvsを使う）． 一度scipy.stats.binomのドキュメントのMethodsの欄に目を通してみるといいかもしれない．

正規性

確率分布は「すべて足して1」にならなければならない．それを二項分布で確かめる．

\[ \sum_{k=0}^n{}_nC_kp^k(1-p)^{n-k} = \{p+(1-p)\}^n = 1 \]

この計算には二項定理を用いている．

期待値と分散

二項分布の期待値は

\begin{align} \mathbb{E}(x) &= \sum_{k=0}^n kP(k) \\ &= \sum_{k=0}^n k\cdot\frac{n\cdot(n-1)!}{k\cdot(k-1)!(n-k)!}p^k(1-p)^{n-k} \\ &= \sum_{k=0}^n k\cdot\frac{n}{k}\cdot{}_{n-1}C_{k-1}p^k(1-p)^{n-k} \\ &= np\sum_{k=0}^n {}_{n-1}C_{k-1}p^{k-1}(1-p)^{(n-1)-(k-1)} \\ &= np\cdot\{p+(1-p)\}^n \\ &= np \end{align}

となる．表裏の出る確率がイーブンなコインを10回投げるとだいたい5回(=10・(1/2))表になる直感にそっている．

分散は

\[ \mathrm{Var}(x)=np(1-p) \]

である．

練習1

二項分布の分散を計算せよ．

期待値と似たような計算で確認できる．

正規分布と中心極限定理

二項分布の試行回数\(n\)を十分大きくしていくと，どうなるだろうか．

コイントスの例で考える．トスの回数\(n\)を1回から100回まで増やしていく． 各\(n\)において，同じ試行を10000回行い，表の出た回数をヒストグラムにとってみる． これは以下のようなスクリプトで実現できる．

import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt

for n in np.linspace(1, 100, 10):
    n = int(n)
    p = 0.5
	# 二項分布の生成
    xs = binom.rvs(n, p, size=10000)
	# キャンバスのクリア
    plt.clf()
	# ヒストグラムの描画（binsはヒストグラムの分割数、あまり気にしなくて良い）
    plt.hist(xs, bins=int(n/2.)+1)
    plt.xlim([0, 100])
    plt.suptitle('n = {}'.format(n))
    plt.savefig('fig{}.png'.format(n))

この結果得られたプロットをGIFアニメーションにしたのが下の画像である．

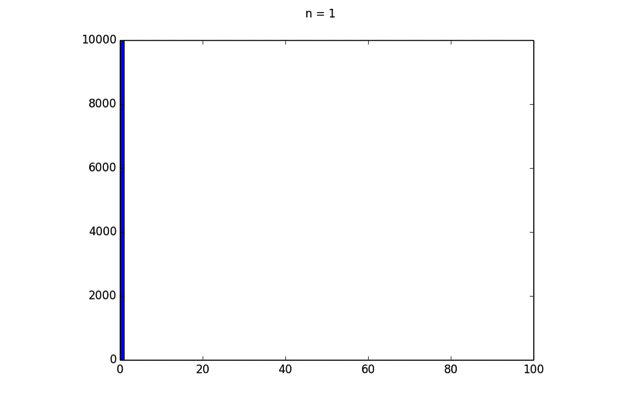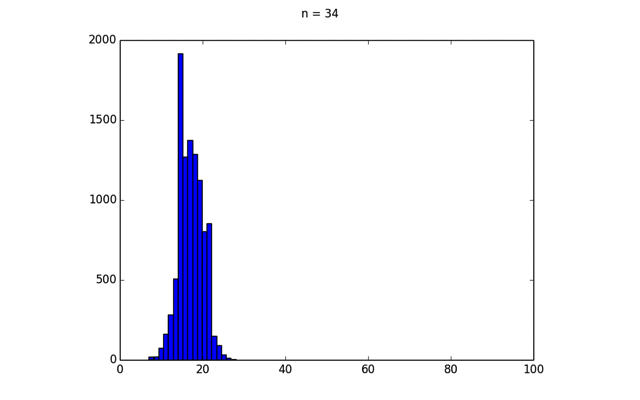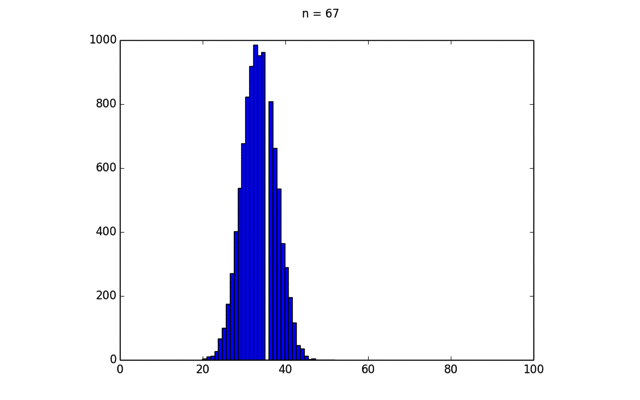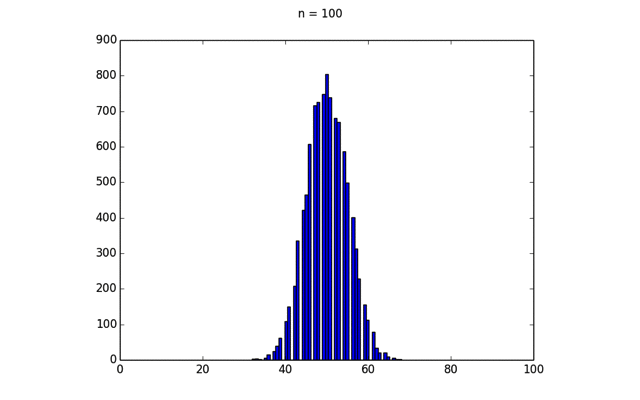
二項分布の近似

このように，二項分布の形状が次第に一定のカーブに近づいていく． この分布は正規分布と呼ばれ，次のような式で表される．

\[ P(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \]

\(\mu\)は平均（＝期待値），\(\sigma\)は分散である．

実際に\(n=100\)のヒストグラムに正規分布を重ねてプロットすると以下のようになる．

正規分布

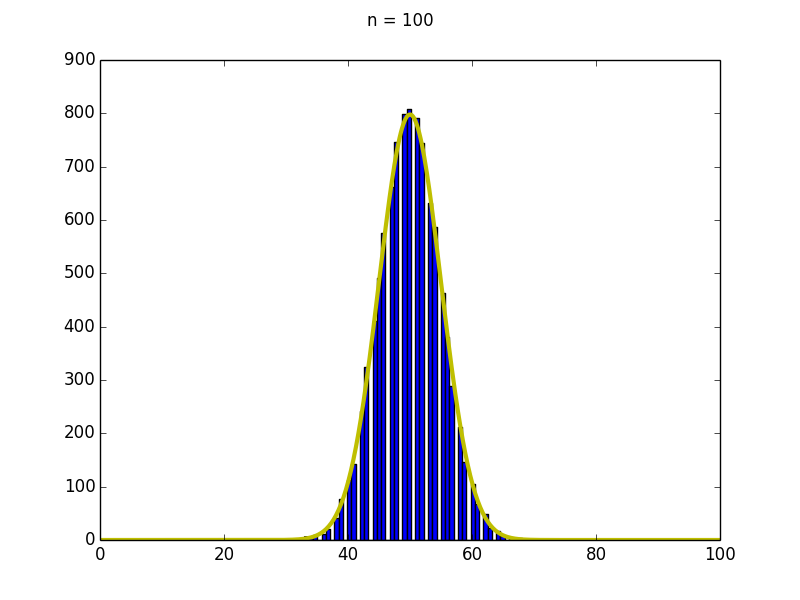
このように二項分布のもとで試行を繰り返すと，その和の分布は次第に正規分布に近づく． この事実は中心極限定理と呼ばれる．中心極限定理の証明は難しいので割愛する． 中心極限定理の存在により，大標本の場合にはまず正規分布を仮定してデータ解析することも多く，正規分布は数ある確率分布でも特殊な位置を占めている．

練習2

サイコロを振って1〜6の目が出る確率は（イカサマされていないという前提で）すべて等しく1/6である． この分布は \(P(x)=\frac{1}{6}\) と書け，一様分布という． 一様分布も二項分布と同様に，正規分布に収束することをスクリプトで確認せよ．

収束はそれなりに速く，\(n=10\)程度でかなり正規分布に近い形になる．

スクリプト例をuniform.pyに示す．

uniform.gifのような結果になれば概ねOKだろう．