今回から本格的に機械学習らしい内容に入っていく．

機械学習で扱う問題のほとんどは識別問題，すなわち与えられたデータの属性を推定する問題であることが多い．

(例)

  • スパムメール判定（受信したメールがスパムなのかそうでないのか）
  • Googleの言語判定（テキストが何語で書かれているのか）
  • YouTubeのおすすめ動画

スパムフィルタ ↑GMailのスパムフィルタ

言語判定 ↑Googleの言語判定

おすすめ動画 ↑YouTubeのおすすめ動画

それは機械学習が必要なのか

昨今の機械学習ブームの影響で，とりあえず機械学習を使ってみたいというケースが増えている（僕もそのクチだ）． ただ，何でもかんでもとりあえず機械学習で識別させておけばいいわけではない． 例えば，自動販売機に投入される硬貨の種類を判定するのにわざわざ機械学習を用いる必要はない． 対象はせいぜい1円玉，5円玉，10円玉，50円玉，100円玉，500円玉の6種類しかないので，rule-basedに記述した方が速い．

機械学習を用いた方が良いのは，処理すべきデータ規模が人力では扱えないほど大きかったり，ruleが曖昧な場合などである． （「スパムメールの基準を書き出せ」と言われたら難しいだろう）

また，機械学習を用いるにしても，徹頭徹尾全て機械学習に頼りきらなければいけない道理はどこにもない． サイボウズ・ラボの中谷秀洋氏に話を伺う機会があったのだが，言語判定をやっていると異言語間で同じ綴りの単語が使われているケース等で，機械学習ではどうしても乗り越えられない壁に当たる時があるのだが，そういう場合は普通にif文一つかませてしまうと精度が上がるそうだ．

言語判定へのいざない - SlideShare

線形識別関数

それでは前置きから本題に入ろう．テキスト処理の例を据えながら説明する． ここでは，ブログ記事のトピックが統計に関連するのかしないのかを判定するようなプログラムを作ることを考えてみよう． まず，記事中に「統計」という言葉が登場していたら機械学習に関連する記事だと判定することにしよう． これを式として表すなら，「統計」という単語の登場回数を\(x\)として，

\[ f(x)=x-1 \]

という識別関数を考え，

\begin{align} f(x)\ge 0 &\Rightarrow \mathrm{related}\\ f(x)\lt 0 &\Rightarrow \mathrm{not\,related} \end{align}

というように書き表せる（自明に見えるかもしれないが丁寧に進める）．

しかし，「統計」という単語が含まれているからといって，必ずしも統計に関する文章であるとは限らない． （例えばこのページには「統計」という単語が登場するが，どちらかといえば天気に関する文章だ） 記事の長さは記事ごとによってまちまちなので，記事に出現する全単語数で割った値を用いた方がよいかもしれない（正規化という）． また，「統計」という単語が登場しなくても「検定」や「有意」という単語が登場しているなら統計に関係あるかもしれない．

これを踏まえて，次は「統計」「検定」「有意」という単語の登場回数を記事中の全単語数で割った値をそれぞれ\(x_1,x_2,x_3\)とし，

\[ f(x_1,x_2,x_3)=x_1+3x_2+2x_3-r \]

という識別関数を考える．relatedとnot relatedの判別基準は先ほどと同様とする． 3や2といった係数は僕が適当に与えたもので，この場合「検定」や「有意」が登場すると「統計」が登場したときよりもrelatedと判断しやすくなる．

今ここで考えている識別関数は，記事から\(\{x_i\}_{i=1}^N\)というパラメータを抽出し，それを線形写像（1次関数）で処理している．

一般化する．

2クラス問題\(C_1,C_2\)を分類する線形識別関数は次のように書ける．

\[ f(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+w_0 \]

識別の基準は

\begin{align} C_1 & \;\mathrm{if}\; f(\boldsymbol{x})\ge 0\\ C_2 & \;\mathrm{if}\; f(\boldsymbol{x})\lt 0 \end{align}

とする．

\(\boldsymbol{x}\)は入力ベクトル，\(\boldsymbol{w}\)は係数ベクトル，\(w_0\)はバイアス項と呼ばれる．

ここでバイアス項を\(\boldsymbol{w}\)の第(N+1)要素に追加し，\(\boldsymbol{x}\)の第(N+1)要素に1を追加すると

\[ f(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x} \]

と書くことができる． こちらの方が一般的には扱いやすいので，以降バイアス項は省略する．

二乗誤差

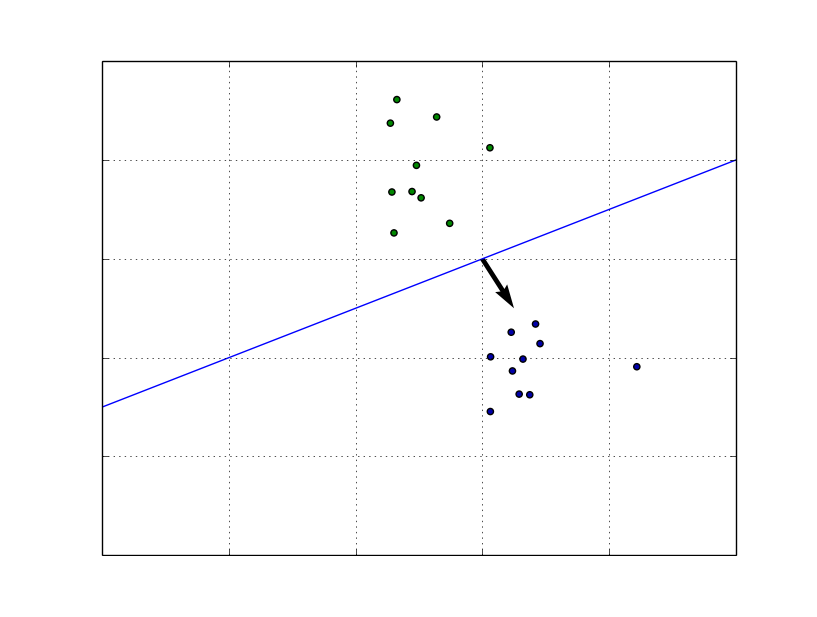
ちなみに，\(\boldsymbol{w}^T\boldsymbol{x}=0\)は\(\boldsymbol{w}\)を法線ベクトルとする超平面の式になる． つまり\(\boldsymbol{w}^T\boldsymbol{x}\)はベクトル\(\boldsymbol{x}\)の超平面からの距離になる．

学習と推定

上記の説明では，人間側が適当に係数をいじっていたが，実際に「検定」を重視したほうがいいのか，「有意」を重視したほうがいいのか，ということはデータを見なければわからない． したがって，コンピュータに大量の「あらかじめ統計に関連するかどうかわかっている」データを処理させ，最適な係数を計算によって求めさせる． これが機械学習のうち，学習のフェーズになる．

学習さえしてしまえば推定は簡単で，「統計に関連するかどうか知りたい」記事のデータについて\(f(\boldsymbol{x})\)の値を計算して，上記の識別の基準にしたがって判断すればよい．

ここで問題になるのは，どのようにしてデータから最適なパラメータを計算するかということになる．ここではシンプルな評価関数として二乗誤差を考える．

最小二乗誤差基準

上の例では識別関数が正のクラスが正の値のときは\(C_1\)，負の値のときは\(C_2\)に分類される． ここで行いたいのは，学習データをコンピュータに与えて，最適なパラメータ\(\boldsymbol{w}\)を計算することである． これを以下のように行う．

学習データに対して，\(C_1\)ならば+1，\(C_2\)ならば-1を返すように\(f(\boldsymbol{x})\)を設計する． そのために二乗誤差\((t_i-f(\boldsymbol{x_i}))^2\)を計算し，その総和が最小になるような\(\boldsymbol{w}\)を計算する． (x_iはi番目の学習データ．t_iはi番目の学習データのラベル値で，{1,-1})

すなわち，最小化すべきは

\[ J(\boldsymbol{w})=\sum_{i=1}^K(t_i-\boldsymbol{w}^T\boldsymbol{x_i})^2 \]

この式は次のように書きなおすことができる．

\[ J(\boldsymbol{w})=\|\boldsymbol{t}-X\boldsymbol{w}\|^2 \tag{6-1} \]

ここで\(\boldsymbol{t}=(t_1 t_2 \cdots t_K)^T\)，

\[ X = \left(\begin{array}{c} \boldsymbol{x_1}^T \\ \boldsymbol{x_2}^T \\ : \\ \boldsymbol{x_K}^T \end{array}\right) \]

最適解

今一度解くべき問題を整理すると，評価関数(6-2)\(J(\boldsymbol{w})\)の最小化である． ここでいきなり最急降下法にかける前に，式の上で計算してみる．

まず\(J(\boldsymbol{w})\)を微分すると

\begin{align} \frac{\partial J}{\partial\boldsymbol{w}} &= \frac{\partial}{\partial\boldsymbol{w}}(\boldsymbol{w}^TX^TX\boldsymbol{w}-\boldsymbol{w}X^T\boldsymbol{t}-\boldsymbol{t}^TX\boldsymbol{w}+\|\boldsymbol{t}\|^2) \\ &= 2X^TX\boldsymbol{w}-2X^T\boldsymbol{t} \\ \end{align}

ここでは制約条件はついていないので，単純に導関数=0とおくと

\[ X^TX\boldsymbol{w}=X^T\boldsymbol{t} \]

これは正規方程式と呼ばれている． したがって

\[ \boldsymbol{w}=(X^TX)^{-1}X^T\boldsymbol{t} \]

という解が得られる．

簡単な例

初めにインストールしたモジュールの中にscikit-learnというモジュールがある． これはPython向けの機械学習モジュールで，様々なアルゴリズムが提供されていたり，サンプルデータが提供されている． ここではiris(アヤメ)のサンプルデータを用いて，最小二乗学習を行ってみる．

irisのロード

sklearn.datasets.load_irisでirisをロードできる．

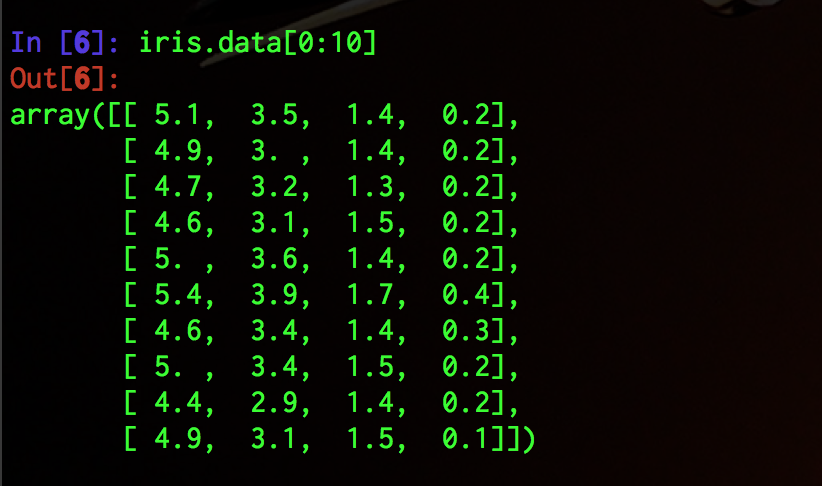
データはこのような4次元データになっている．

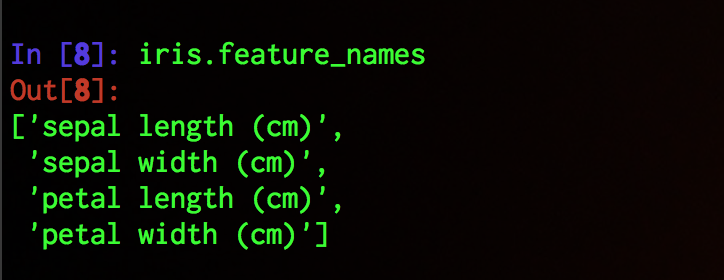
各次元はこのような特徴を表現している．

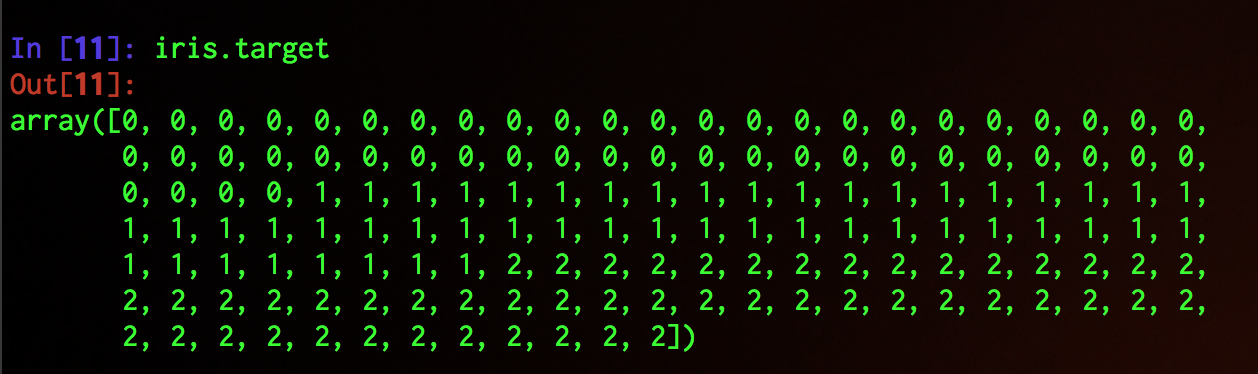
target

各データのラベル値はこのようになっている．

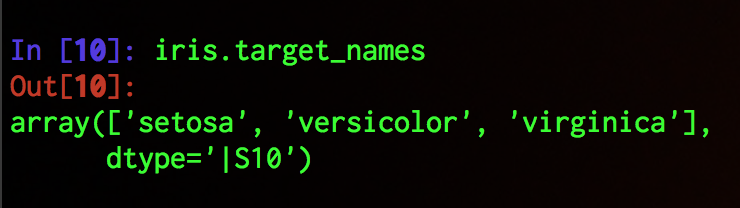
ラベル値はそれぞれsetosa, versicolor, virginicaというアヤメの種類と対応している．

現時点では2クラス分類しかできないので，「setosaかそうでないか」を推定するプログラムを書いてみる．

#!/usr/bin/env python
# coding: utf-8

import numpy as np
from sklearn import datasets
from sklearn import cross_validation
from sklearn import metrics

iris = datasets.load_iris()
data = iris.data[0:100]
target = [1 if t == 1 else -1 for t in iris.target[0:100]]

train_x, test_x, train_y, test_y = cross_validation.train_test_split(data, target, test_size=0.2)

# 最小二乗法で学習
w = np.linalg.inv(train_x.T.dot(train_x)).dot(train_x.T).dot(train_y)

# 最小二乗法で推定
pred_y = np.array([1 if w.dot(x) > 0 else -1 for x in test_x])

# テストデータに対する正答率
print metrics.accuracy_score(test_y, pred_y)

例

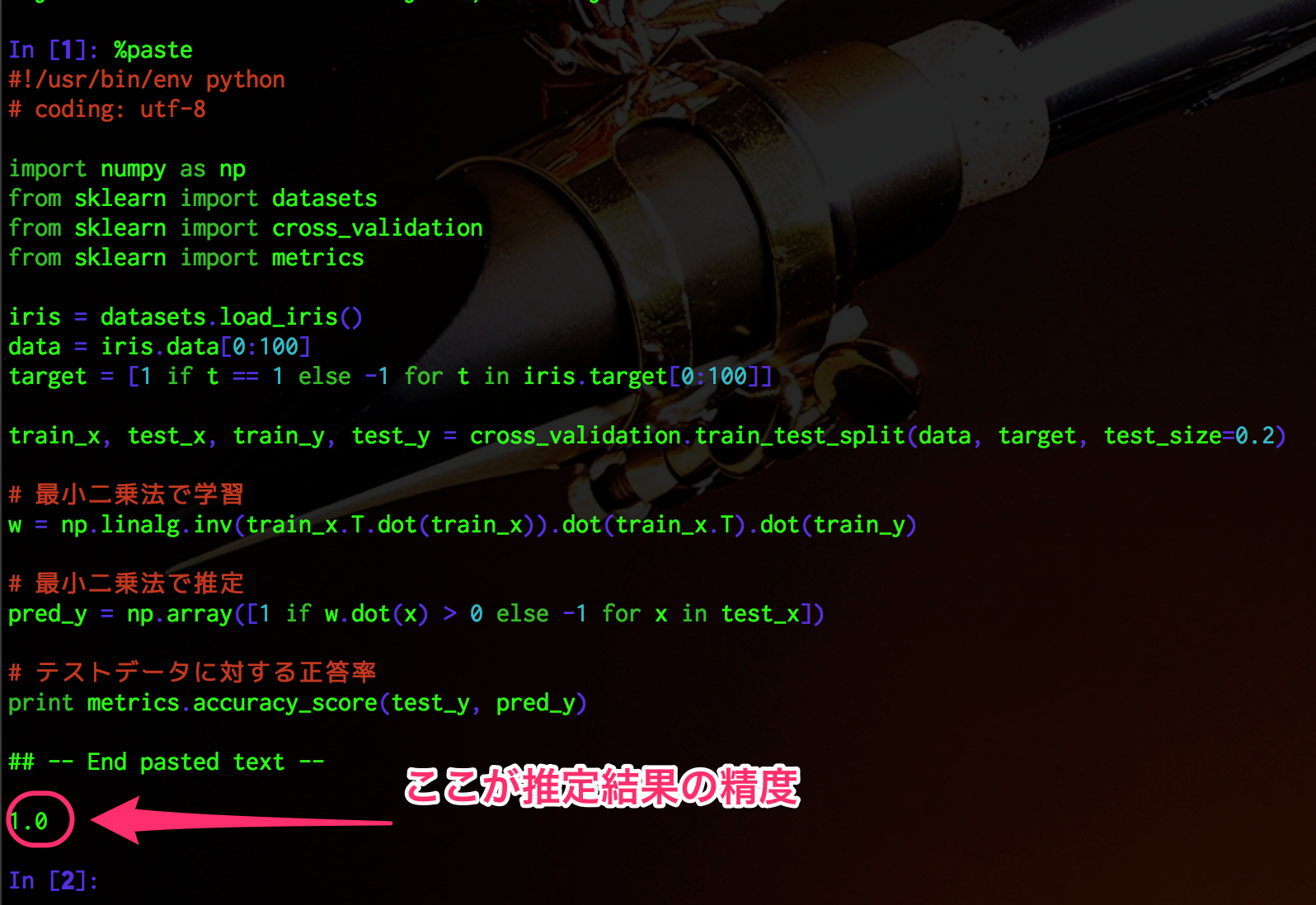
train_x, test_x, train_y, test_y = cross_validation.train_test_split(data, target, test_size=0.2)

の行はirisを(学習データ):(テストデータ)=4:1に分割している(test_size=0.2)．train_x, train_yを使って\(\boldsymbol{w}\)を推定し，できた識別器にtest_xをかけてpred_yを

pred_y = np.array([1 if w.dot(x) > 0 else -1 for x in test_x])

で得て，そのうち何%がtest_yと一致しているかをsklearn.metrics.accuracy_scoreを用いて

print metrics.accuracy_score(test_y, pred_y)

の行で計算している．

この程度であれば100%の精度を達成することができる．