#07 ニューラルネットワーク

ニューラルネットワークは線形識別モデルの一つで，生体の神経回路（シナプスは他のシナプスから電気信号を入力として受け付け，ある一定量以上の刺激を受けたら発火して次のシナプスへ出力する）を模したモデルである． 最初期のものは60年以上前に提案されたもので，それ以降現在に至るまでパーセプトロン，ボルツマンマシン，オートエンコーダ等多数のアルゴリズムが考案され，昨今のDeep Learningのブームにつながっている．

神経回路を模した，といっても実際には特徴量を数学的に重み付けして評価関数を最適化する，今までのような統計的解析手法にすぎない． しかし，多層パーセプトロンや深層学習のように多層にすればするほど，モデルの表現能力が飛躍的に向上することがわかったため，画像処理や音声処理をはじめとした多くの分野で応用されるようになっている．

今後の分科会はニューラルネットワークを中心に，およそ3回でDeep Learningに到達する予定である．

単層パーセプトロン

一般的にグラフ理論におけるネットワークとは，双方向かつ閉路等も含む，ノードとエッジとフローから構成されるものである． パーセプトロンとは，ニューラルネットワークの中で一方向なものである． 順伝播型ネットワークとも呼ばれる．

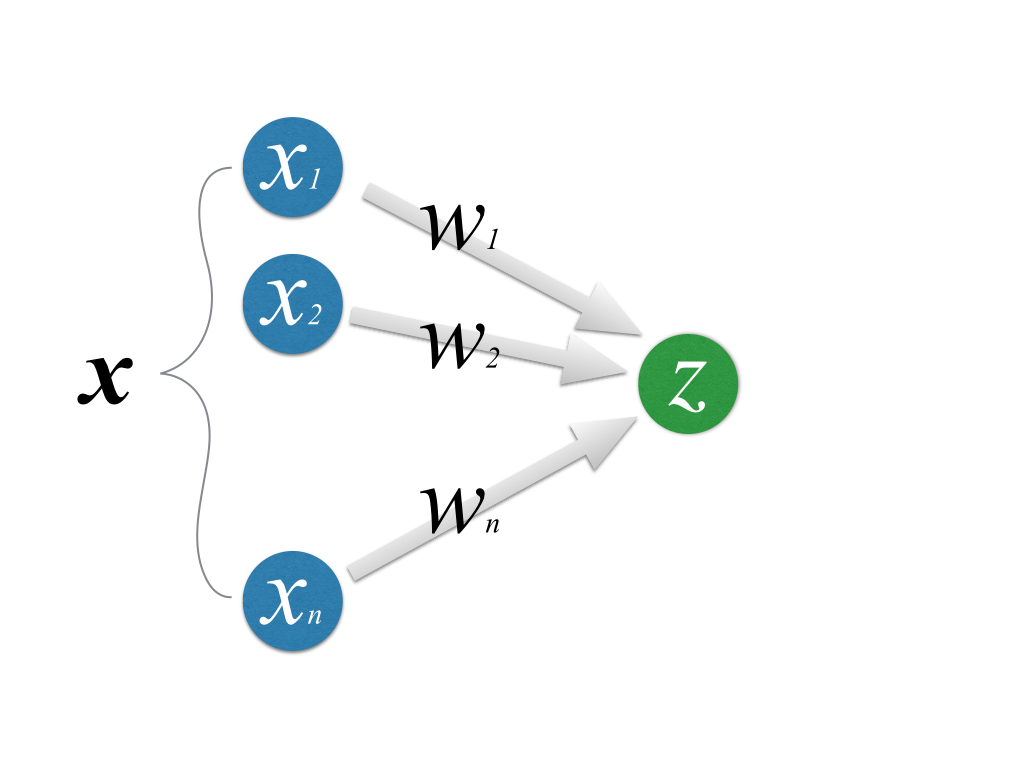
この図で，最も右のノードは

という入力を受け付ける．この部分は「他のシナプスから電気信号が伝わってくる」部分に対応する．

「ある一定量以上の刺激を受けたら発火して出力する」ことを表現するために入力\(u\)を次の関数にかける．

これはhinge関数と呼ばれる階段上の関数である．

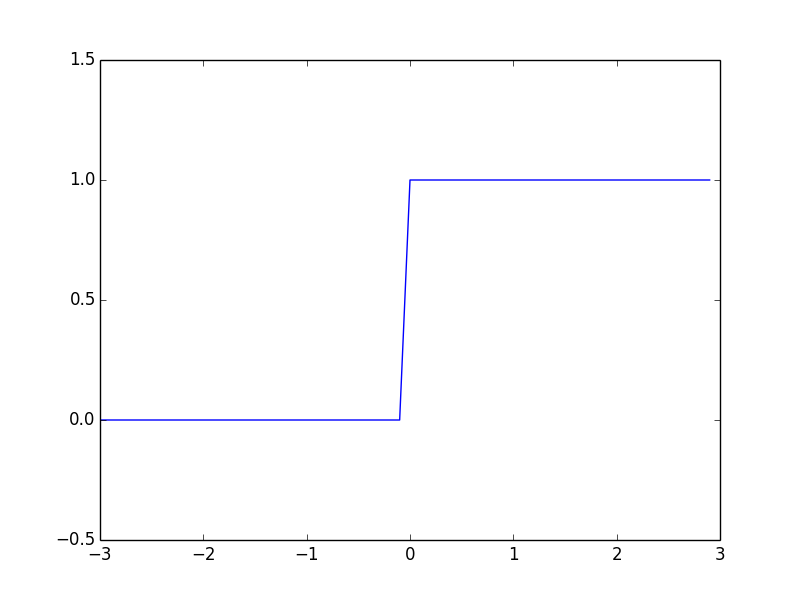
この関数によって出力を\(z=f(u)\)と得ると，純粋に「ある一定値を超えると発火する」ことを実現できるが，実際には連続値をとりhinge関数に形状が似たLogistic関数が利用されることが多い．

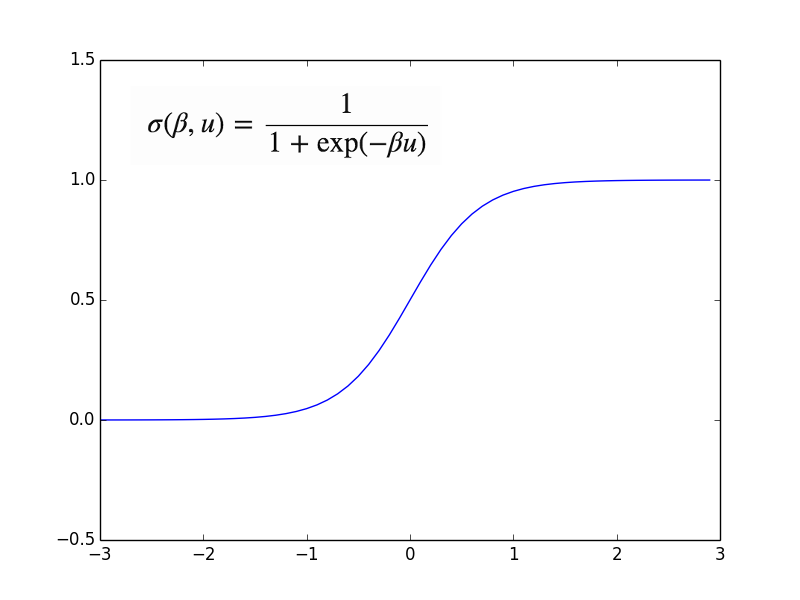
\(\beta\)はパラメータ（正数）であり，大きければ大きいほどロジスティック関数の勾配は急になる．

このようにパーセプトロンの出力にかける関数のことを活性化関数という．

多層パーセプトロン

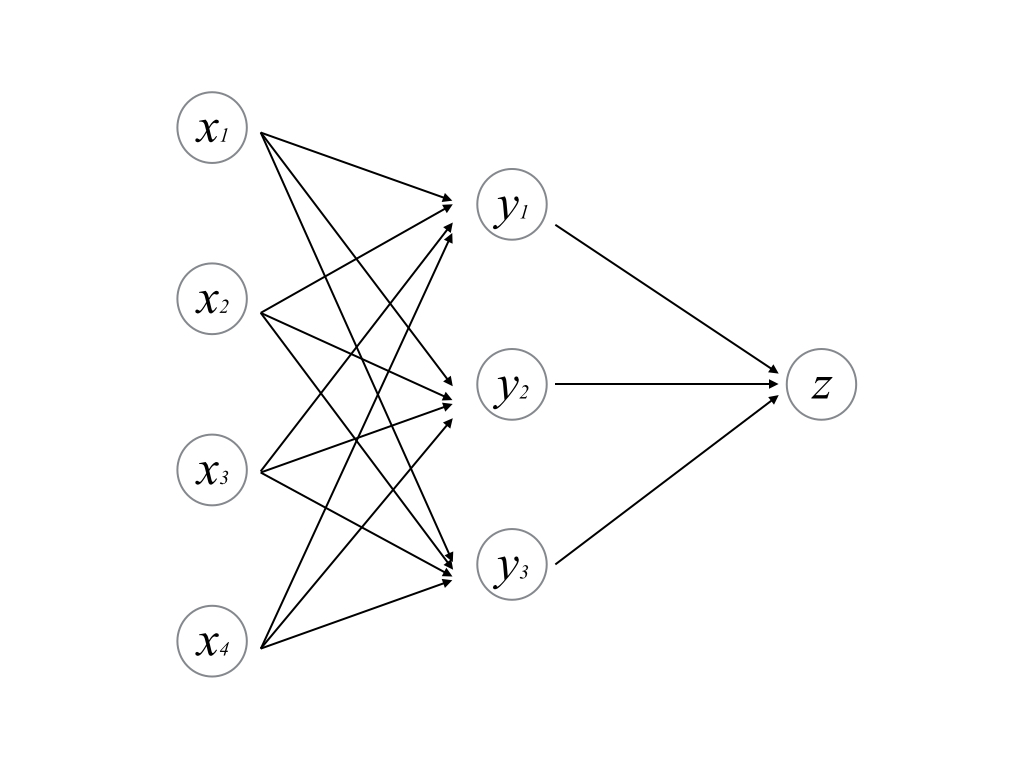
多層パーセプトロンは，単層パーセプトロンを重ねたものである． 入出力と活性化は基本的に単層パーセプトロンと同じである．

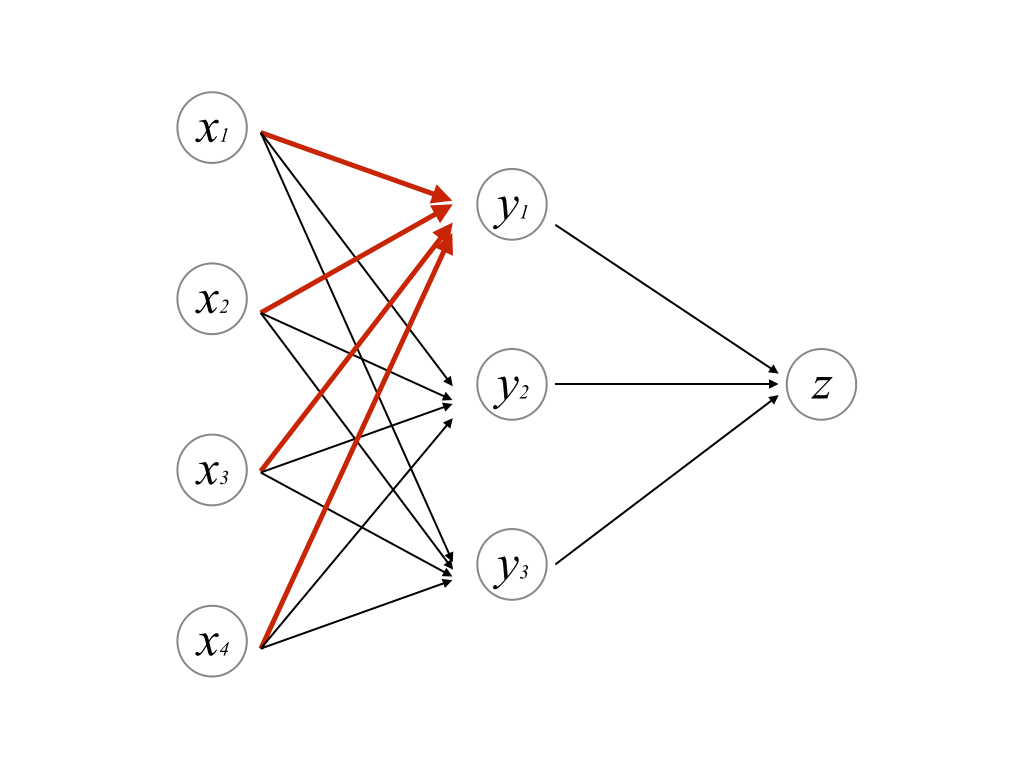
このように部分的に抽出すると，単層パーセプトロンとして見做すことができる．

これからよく登場するのは2層の多層パーセプトロンになる． 多層になればなるほど学習時のパラメータの推定が計算量の面から困難になるからである． 2層のパーセプトロンにおいて，中間層の活性化関数にロジスティック関数，出力層の活性化関数に恒等関数\\(f(x)=x\\)を用いる．

パーセプトロンを多層にすることで一般的に表現能力が上がり，多彩な分類・認識を行うことができる． しかし，同時にパラメータ推定を行うのに飛躍的にリソースが増加する． （その問題を上手く解決したのがDeep Learningであるといえる）