#07ではパーセプトロンを紹介した.
ここではパーセプトロンを用いた学習を紹介する.
そもそも教師あり学習における学習とは,#06で触れたようにデータセット
\[
\mathcal{D}=\{(\boldsymbol{x_1},t_1),\cdots,(\boldsymbol{x_N},t_N)\}
\]
が与えられて,各学習データ\((\boldsymbol{x_i},t_i)\)に対して\(z_i\)という出力が得られるとき,誤差関数を最小にするようにパラメータを推定することであった.
また,一般的に誤差関数として二乗誤差関数
\[
E(\boldsymbol{w})=\frac{1}{2}\sum_{i=1}^N|t_i-z_i|^2
\]
が用いられることが多い.(先頭の1/2は微分したときに係数が消えるようにつけてあるだけ)
#06では単純な線形識別関数を用いて識別していたので,解析的に二乗誤差関数の最小化を行うことができた(正規方程式に落とし込める).
しかし,パーセプトロンが少し複雑になると解析的に解くのは難しくなるので,#04で紹介した最適化手法の勾配法を用いて最小化する.
\[
\boldsymbol{w}^{(n+1)}=\boldsymbol{w}^{(n)}-\eta\frac{\partial E}{\partial\boldsymbol{w}}
\]
という更新式でパラメータ\(\boldsymbol{w}\)を更新するアルゴリズムであった.
気をつけたいのは,このとき必要な学習データは事前にすべて読み込ませなければいけないという点である.
なぜなら,二乗誤差関数Eを計算するときにはすべての学習データが必要だからである.
このように学習データをまとめて学習する方法は__バッチ学習__と呼ばれている.
ここから紹介するのは,学習データを少しずつ(極端には1つずつ)学習する方法であり,__オンライン学習__と呼ばれる.
確率的勾配降下法(SGD)
確率的勾配降下法(Stochastic Gradient Descent = SGD)とは,ランダムに学習データを1つ選んで誤差関数を計算し,その勾配方向にパラメータを修正する操作を反復する手法である.
今,\(k+1\)回目のパラメータ更新において\(n_{k+1}\)番目の学習データを選んだとき,更新式は以下のようになる.
\[
\boldsymbol{w}^{(k+1)}=\boldsymbol{w}^{(k)}-\eta\frac{\partial}{\partial\boldsymbol{w}}\left(\frac{1}{2}|t^{(n_{k+1})}-z^{(n_{k+1})}|^2\right) \tag{8-1}
\]
すべての学習データに対する誤差関数ではなく,\(n_{k+1}\)番目の学習データに対する誤差関数
\[
E^{(n_{k+1})}(\boldsymbol{w})=\frac{1}{2}|t^{(n_{k+1})}-z^{(n_{k+1})}|^2 \tag{8-2}
\]
の勾配方向にパラメータを更新している.
SGDの利点
SGDにはナイーブな勾配法に比べて以下のような利点があげられる.
- 局所最適解にトラップしにくい(勾配法の初期値依存問題への解決)
- 冗長な学習データがある場合,勾配法よりも学習が高速
- 学習データを収集しながら逐次的に学習できる
誤差逆伝播法(Back Propagation)
原理的には(8-1)の更新式を用いれば,SGDにより最適パラメータが推定できる.
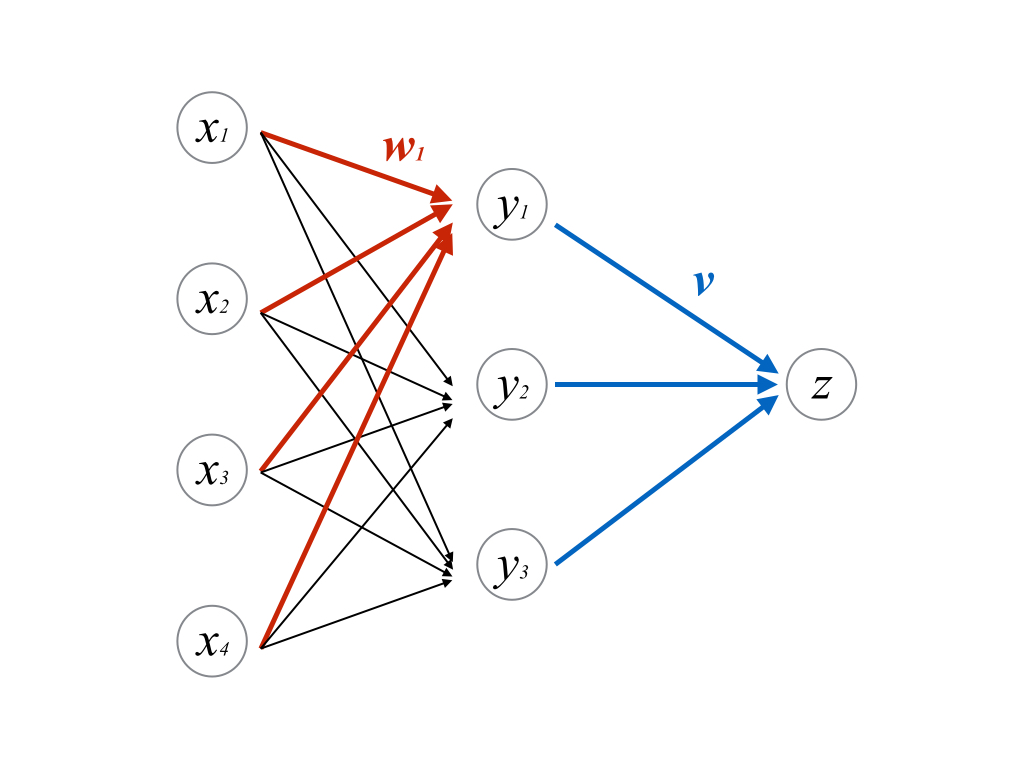
今回は1段目はロジスティック関数を活性化関数に用い,2段目では恒等関数\(f(x)=x\)を活性化関数に用いるものとする.
図のパーセプトロンに対して(8-2)の微分を計算しようとすると,2段目(青い部分)は
\begin{align}
\frac{\partial E^{(n)}}{\partial\boldsymbol{v}}
&= (z^{(n)}-t^{(n)})\frac{\partial z^{(n)}}{\partial\boldsymbol{v}} \\
&= (z^{(n)}-t^{(n)})\frac{\partial}{\partial\boldsymbol{v}}(\boldsymbol{v}^{\mathrm{T}}\boldsymbol{y}) \\
&= (z^{(n)}-t^{(n)})\boldsymbol{y}
\end{align}
1段目は(\([x_1, \cdots,x_4]\mapsto y_1\),すなわち赤い部分にのみ着目すると)
\begin{align}
\frac{\partial E^{(n)}}{\partial\boldsymbol{w_1}}
&= (z^{(n)}-t^{(n)})\frac{\partial z^{(n)}}{\partial\boldsymbol{w_1}} \\
&= (z^{(n)}-t^{(n)})\frac{\partial}{\partial\boldsymbol{w_1}}(\boldsymbol{v}^{\mathrm{T}}\boldsymbol{y}) \\
&= (z^{(n)}-t^{(n)})\boldsymbol{v}\frac{\partial\boldsymbol{y}}{\partial\boldsymbol{w_1}} \\
&= (z^{(n)}-t^{(n)})\boldsymbol{v}\frac{\partial}{\partial\boldsymbol{w_1}}(\sigma(\boldsymbol{w_1}^{\mathrm{T}}\boldsymbol{x})) \\
&= (z^{(n)}-t^{(n)})\boldsymbol{v}\left(\frac{\partial\sigma(u)}{\partial u}\right)_{u=\boldsymbol{w_1}^{\mathrm{T}}\boldsymbol{x}}\frac{\partial(\boldsymbol{w_1}^{\mathrm{T}}\boldsymbol{x})}{\partial\boldsymbol{w_1}^{\mathrm{T}}} \\
&= (z^{(n)}-t^{(n)})\boldsymbol{v}\left(\frac{\partial\sigma(u)}{\partial u}\right)_{u=\boldsymbol{w_1}^{\mathrm{T}}\boldsymbol{x}}\;\;\boldsymbol{x}^{\mathrm{T}} \\
&= (z^{(n)}-t^{(n)})\sigma'\boldsymbol{v}\boldsymbol{x}^{\mathrm{T}}
\end{align}
ただし\(\sigma\)はロジスティック関数とする.
\[
\sigma(x)=\frac{1}{1+\exp(-x)}
\]
ここで重要なのは,どちらも
\[
\frac{\partial(\mathit{Error Function})}{\partial(\overrightarrow{\mathit{Param}})}\propto(\mathit{Error})\times(\overrightarrow{\mathit{Input}})
\]
という形になっているという点である(\(z_n-t_n\)が誤差,\(\boldsymbol{x,y}\)が入力ベクトル).
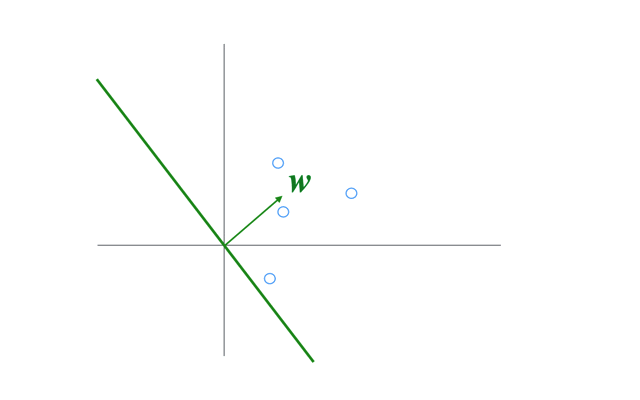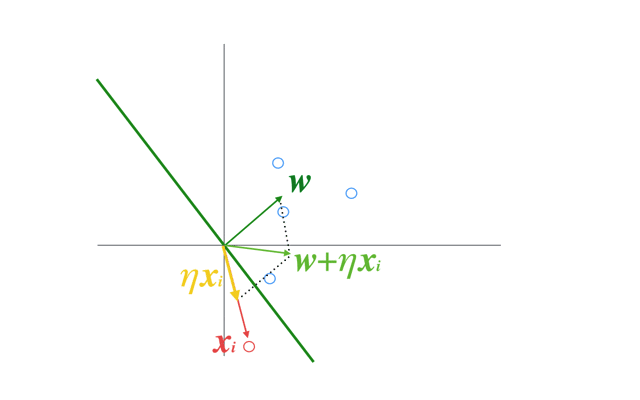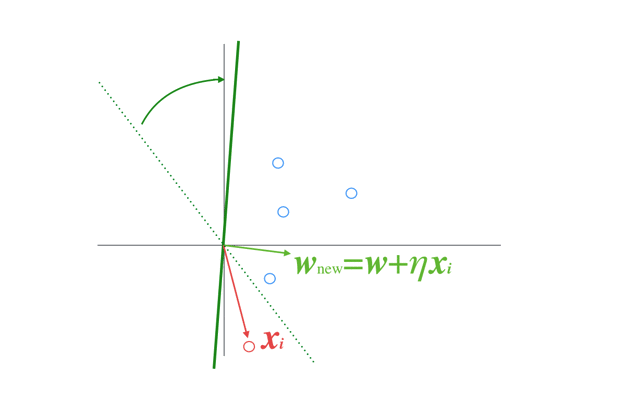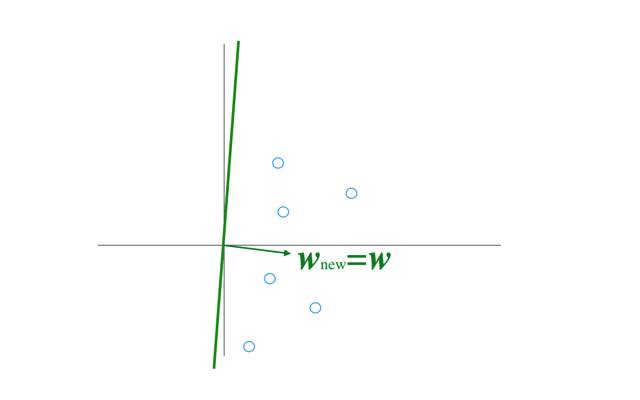
イメージとしてはこのGIFのように,入力ベクトルの方向にパラメータを修正することを繰り返すことになる
(このGIFでは固定係数\(\eta\)による更新だが,ここでは固定係数ではなく誤差がかかった変動係数である).
多層パーセプトロンのテスト
digit.pyはscikit-learnに含まれるMNIST datasets(手書きの数字)を多層パーセプトロンで分類している.
自前実装なのでパラメータの初期値の取り方や中間層数の取り方を適当にやってしまっている.
初期値ベクトルの取り方についてはUnderstanding the difficulty of training deep feedforward neural networksを参照するとよさそう.

