オートエンコーダ

#07，#08で扱った多層パーセプトロンは，このような形状をしていた．

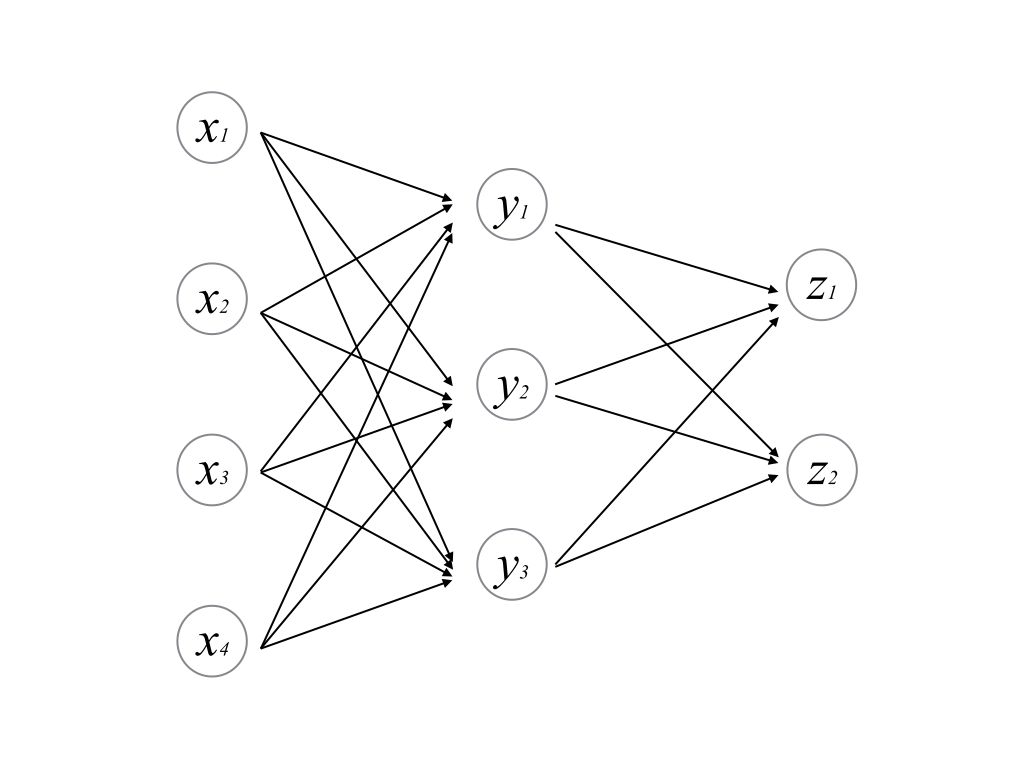
多層パーセプトロン

入力ベクトルとして\(\boldsymbol{x}\)を与え，教師ベクトルとして\(\boldsymbol{z}\)を与えて，誤差関数を最小化することで学習を行った． （#07での説明では教師信号は\(z\)というスカラーで説明したが，これをベクトルに拡張するのは難しくない）

ここで，教師ベクトルを次のようにとってみる．

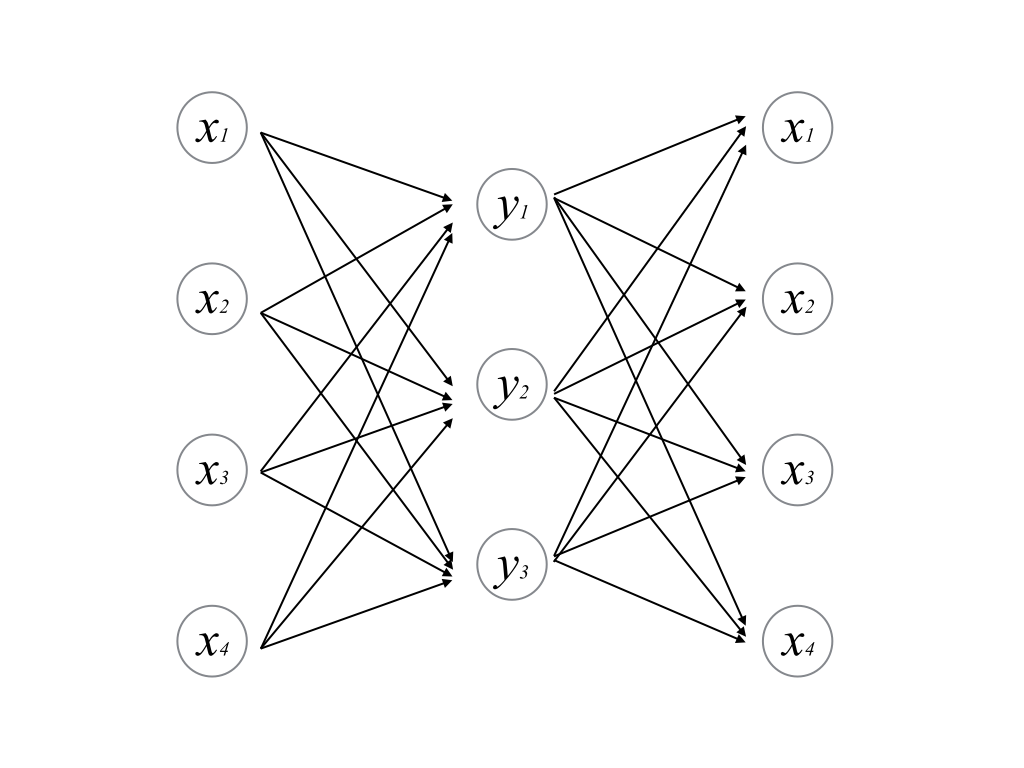
オートエンコーダ

すなわち，教師ベクトル=入力ベクトルである． このパーセプトロンは，入力ベクトルを与えると出力として自分自身を復元することが期待される．

しかし，目的としているのは入力を復元することではなく，中間層の出力である． 中間層のノード数が入力層よりも少ない状態で入力を復元することができれば，より少ない情報量(=低次元)で入力データを表現できていることになる． 言い換えれば，入力データの冗長性を上手に排除することができる．

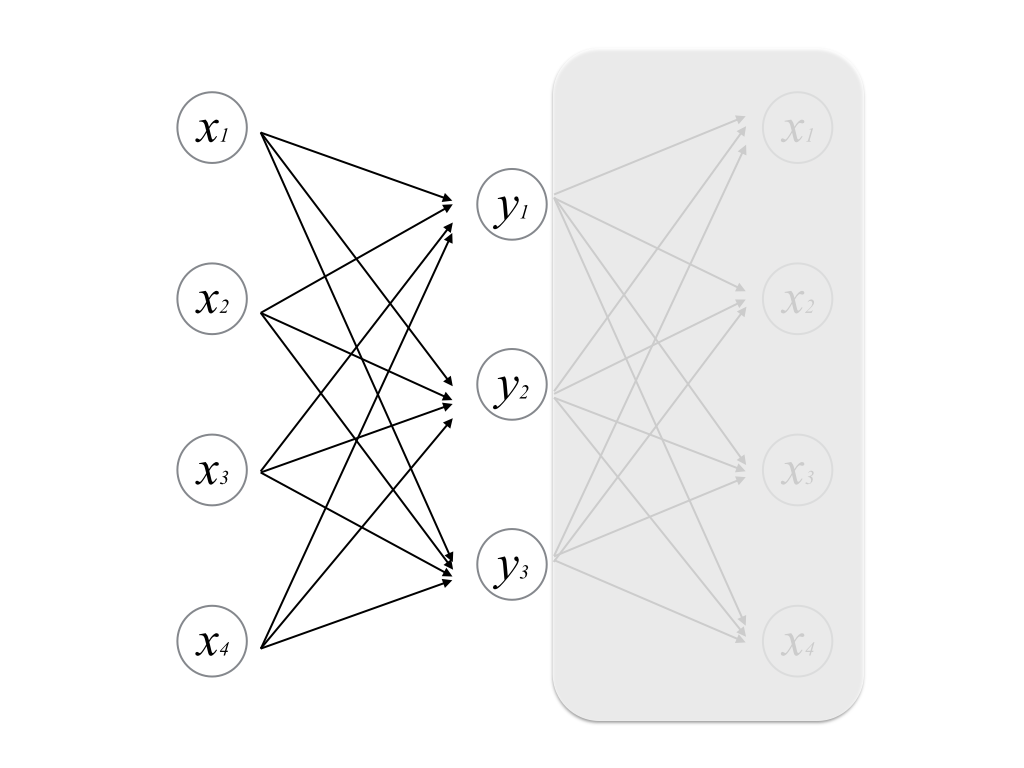
オートエンコーダの中間層

このようなパーセプトロンはオートエンコーダ(自己復号化器，AutoEncoder)と呼ばれる．

オートエンコーダと主成分分析の関係

学習データの次元を削減したいというのは，元々機械学習の分野ではよく行われてきたことである． 数学的には一般次元で問題を定式化して解析的に解くことはできるが，コンピュータサイエンスの視点から見るとたとえ一般次元で定式化されていても次元が大きすぎると有限時間で計算が終わらないので，次元削減したいというのは自然な考えである． （「次元の呪い，The curse of dimensionality」という言葉がよく用いられる） オートエンコーダ以外にも線形代数や統計でよく用いられてきた主成分分析(principal component analysis, PCA)という手法を簡単に紹介する．

主成分分析

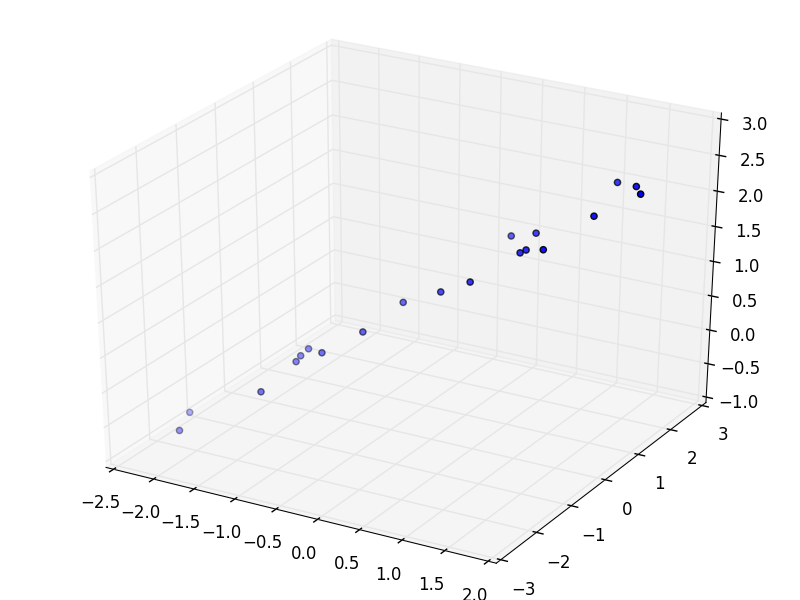
3D空間中のデータ

3D空間中にこのようなデータ列があったとする（本来は一般次元で考えるべきだが，視覚化のため3次元とする）． 今，このプロットは通常通り(x,y,z)の直交座標系をとっている． ちなみに，データ列は

\[ x=y=\frac{z-1}{0.8} \]

という直線上にガウシアンノイズを乗せたものである．

ここで，「このデータ列を最もよく表現できる軸」をとることを考える． データ列は直線上にのっているのだから，この直線の方向ベクトル

\[ \boldsymbol{n}=(\begin{array} 00.5 & 0.3 & 1 \end{array}) \]

を軸としてとるとデータをよく表現できる．

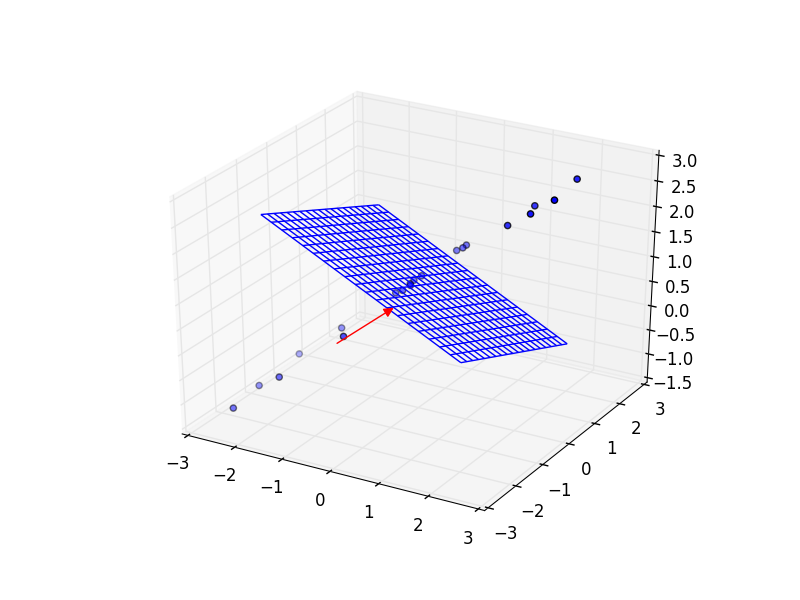
軸の取り方

(縮尺がうまくいかなかった)

実際には勿論データ列の式は天下りには与えられないので，解析的に推定する必要がある．これを数学的に考察する．

今とった軸は，データ列をよく表現できる軸，すなわちデータ列の分散が最大になるような軸である． 言い換えると，データ\(\boldsymbol{x_i}\)をベクトル\(\boldsymbol{n}\)に射影した値\(\boldsymbol{n}^{\mathrm{T}}\boldsymbol{x_i}\)が最もばらつくような\(\boldsymbol{n}\)を求める． すなわち，制約\(|\boldsymbol{n}|=1\)の下で評価関数

\[ J=(\boldsymbol{n},\lambda)=\sum_{k=1}^K(\boldsymbol{n}^{\mathrm{T}}\boldsymbol{x_k})^2+\lambda(1-|\boldsymbol{n}|^2) \]

を最大化する（Lagrangeの未定乗数法）．

計算は割愛して，評価関数Jの極値条件は

\[ R\boldsymbol{n}=\lambda\boldsymbol{n} \tag{9-1} \]

である．ただし

\[ R=\sum_{k=1}^K\boldsymbol{x_kx_k}^{\mathrm{T}} \]

で，分散・共分散行列という（単なる分散は1次元で，共分散行列は一般次元への拡張）．

式(9-1)からわかることは，データ列の分散・共分散行列に対する固有値問題の解が，データ列を最もよく表現するということである．

ここでとったベクトル\(\boldsymbol{n}\)を法線ベクトルとする平面は，元の3次元空間の中でデータ列の分散が最も小さくなる平面である． この平面は\(\boldsymbol{n}\)に対する直交補空間と呼ばれる． 直交補空間内で同様の操作によってさらに軸をとり，その直交補空間内で同様の操作を行い，…を繰り返して軸を次々ととっていく． この解析手法を__主成分分析(principal component analysis, PCA)__と呼ぶ．

主成分分析の本質は次元削減にある． 元のデータの次元が大きすぎるとき，上述の通り何らかの手段によって次元削減したい． そのようなときにデータ列を最もよく表現する順に軸を元の次元より少なくとれば，元のデータの情報をうまく保持しつつ次元を落とすことができる． しかしここで注意しなければならないのは，主成分分析の過程では次元とともに情報量も落ちるので，一般には認識精度は低下する．

オートエンコーダとの関係

主成分分析でとった\(M\)個の固有値ベクトルを行ベクトルとして格納した行列\(\Gamma\)は，次の最小化問題の解になっている．

\[ \min_\Gamma\sum_{k=1}^K|\boldsymbol{x_k}-\Gamma^{\mathrm{T}}\Gamma\boldsymbol{x_i}| \]

一方，中間層の活性化関数が恒等関数であるようなパーセプトロンは，

  • 中間層出力: \(W\boldsymbol{x_k}\)
  • 出力層出力: \(W^{\mathrm{T}}W\boldsymbol{x_k}\)
  • 教師ベクトル: \(\boldsymbol{x_k}\)
  • 誤差: \(\boldsymbol{x_k}-W^{\mathrm{T}}W\boldsymbol{x_k}\)

であるから，\(\Gamma\leftrightarrow W\)と対応付けると主成分分析と同じ問題に落とし込める．

#10で実際に作成するオートエンコーダは中間層の活性化関数がロジスティック関数なので完全に主成分分析と同じわけではないが，次元削減の基本的な概念は主成分分析をイメージすると良い．

【参考】Neural networks and principal component analysis