パーセプトロンの層数を増やせば多彩な表現力が得られ，Deep Learningの基本的な考え方は多層のパーセプトロンをどのように上手に収束させるかということにある． #10ではオートエンコーダを用いた事前学習によって，良いパラメータに収束しやすい初期値を得ることを考えた． この節では，ニューラルネットワークに依らない，学習における一般的なテクニックをいくつか紹介する．

機械学習における問題点

過学習・過適合

過学習

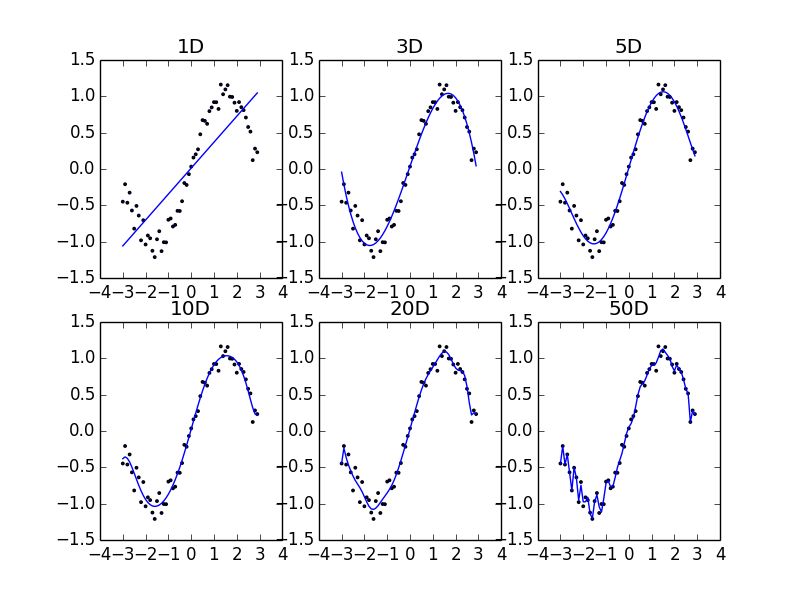
上図は\(y=\sin(x)\)の形状に分布するデータ列を表現するのに，それぞれ1, 3, 5, 10, 20, 50次元の多項式でフィッティングした結果である．

1次関数は線形なので，正弦曲線状にフィッティングするには表現力が不足している． 3次関数くらいになるとフィッティングに十分な表現力を持つことがわかる． しかし，あまりに次元が大きくなりすぎるとデータ列を忠実に通るような曲線になるようにフィッティングされてしまうので，正弦曲線から離れてギザギザになってしまう．20次元や50次元の結果はそれが顕著で，これは望むべき結果ではない． このようにあまりに忠実に元データを再現している状態を__過学習(過適合, overfitting)__という．

一般に，統計モデルの表現力(=パラメータ数)とその尤もらしさは常にtrade-offの関係にある．

計算の難しさ

機械学習は，学習データを使ってモデルのパラメータを計算決定することである． 一般的にパラメータを増やせば表現力が上がり，学習データ量を増やせば学習精度は向上するが，計算量が飛躍的に向上する（前者は特に「次元の呪い」と呼ばれる問題である）．

また，何度も触れている通り，勾配法(#04参照)を用いてパラメータ更新をする際には初期値の選び方が問題になる． 初期値によっては局所解にトラップしてしまうし，最悪の場合計算が収束しない場合もある．

勾配法以外でも，オンライン学習でパラメータを更新する回数が多くなればなるほどパラメータがオーバーフロー・アンダーフローする問題は依然存在する．

様々な解決策

正規化(Normalization)

例えば顔画像認識をする際に，撮影した顔画像写真の光源の当たり方が写真によって違っていた場合，学習に悪影響をおよぼす可能性がある． 文字認識をする際に，人によって文字の形が正方形に近かったり縦長の長方形に近かったりすることがあるが，これもアスペクト比を統一するのが望ましい． このように学習に関係ないデータ間の差異を，学習に影響を及ぼさないように取り除くことを__正規化__という．

Web上の情報では正規化を後述の正則化と取り違えているものもあるので注意を要する．

【参考】ご注文は機械学習ですか？ - kivantiumの活動日記

早期終了(early stopping)

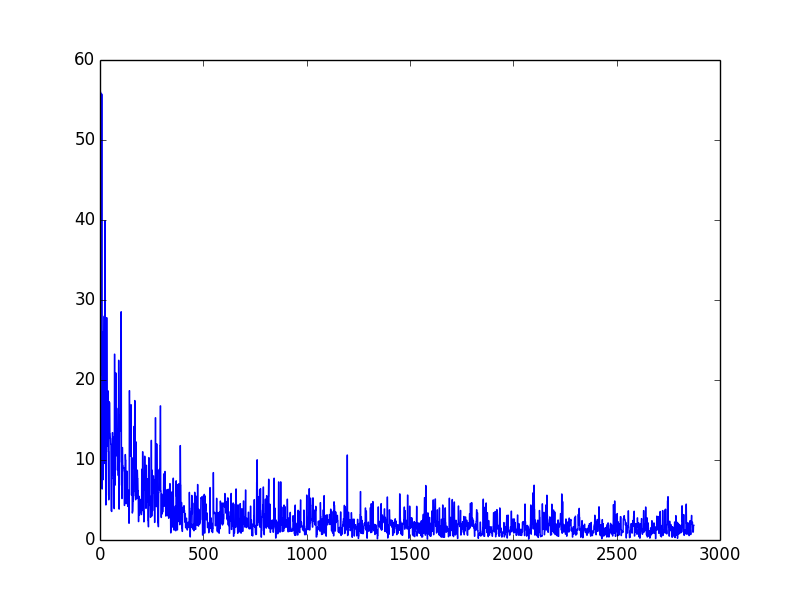
誤差の推移

SGDを用いて学習をするとき，ある一定量以上のデータを学習すると学習がそれ以上あまり進まなくなってくる． 上図はオンライン学習で1データずつ学習した時の，横軸に既に学習したデータ数，縦軸にその時点での推定誤差をプロットしている． この場合，500データ以上になると誤差があまり変わらなくなるので，このあたりで学習を打ち切ることで高速に学習を終えることができる．

なお，これは手書き数字(digits)認識のエラー推移である．

グリッドサーチ

機械学習のモデルには様々なパラメータがある． 例えば，本分科会で扱っている多層パーセプトロンでも

  • 各層のノード数
  • 活性化関数(シグモイド関数, tanh等)の傾斜パラメータ
  • 学習率

といったパラメータがある．このパラメータによって学習の収束がうまくいくかどうか，そして学習自体の精度が決まってくるため，パラメータチューニングは重要な作業になる．

パラメータチューニングで一般的に用いられるのが__グリッドサーチ__という手法である．

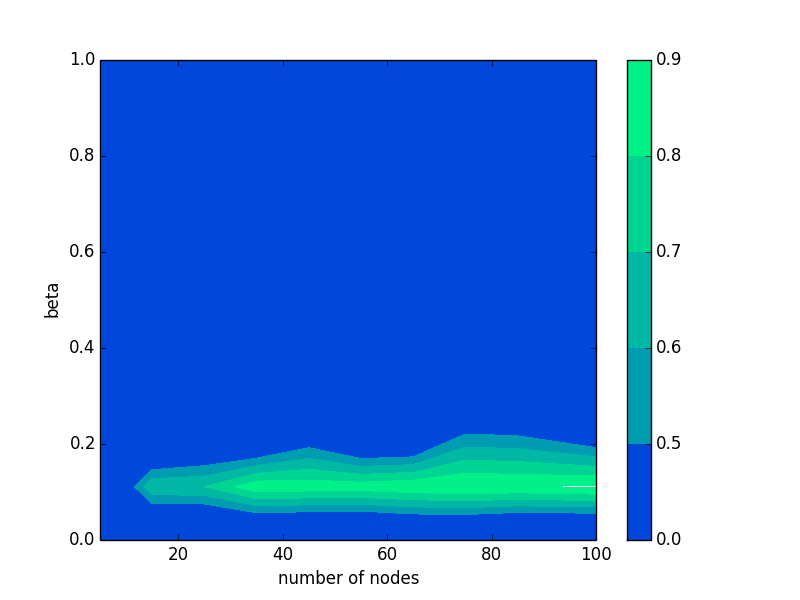
グリッドサーチ

上図は手書き数字認識を2層のパーセプトロンで行った時のグリッドサーチの結果であり，横軸は中間層のノード数，縦軸は活性化関数としてとったシグモイド関数の傾斜パラメータ\(\beta\)の，推定精度のコンターマップである． グリッドサーチという名前は付いているが，やっていることは単純で，チューニングしたいパラメータをある範囲の中で変化させながら学習器を作り，精度を測定するだけである． 単純ではあるが，上図からわかるようにきちんとパラメータチューニングをするかしないかで，同じアルゴリズムでも精度が大分変わってしまう．

このソースコードはgrid_search.pyに示した．

次元削減(次元圧縮)

元の学習データの次元数が大きすぎる場合は，特徴抽出したり，次元削減をして計算量を減らすことを考えるとよい．

特徴抽出

特徴抽出は，元のデータの特徴を捉えて必要な情報だけを抽出する手法である． 上の画像は#01で提示したもので，元画像は400x400=16000画素あるが，勿論16000画素あっても不必要な情報が多く学習に時間がかかりすぎてしまう． 20x20のセルに落としこむことによって，学習精度を保ちつつ(必要な特徴を残しつつ)次元数を元の2.5%まで落とすことができる．

次元削減には様々なアルゴリズムがある．この分科会では既に#09でオートエンコーダと主成分分析を取り上げている． 他にもSVMで用いられるカーネル主成分分析等があるが，詳細についてはこれ以上は詳しく述べない．

正則化(Regularization)

過学習の原因はモデルの自由度(パラメータ数)が大きいことに起因する．だからといって，自由度を下げるとモデルの表現力が低下してしまい，必要な情報をうまく表すことができない． そこで，パラメータになんらかの制約を加えることを考える． これまで考えていた誤差関数は

\[ E(\boldsymbol{w})=\frac{1}{2}||\boldsymbol{y}-\boldsymbol{t}||^2 \]

の形をしたものであった．この右辺に__正則化項__を加える．

\[ E(\boldsymbol{w})=\frac{1}{2}||\boldsymbol{y}-\boldsymbol{t}||^2+\lambda||\boldsymbol{w}||^p \]

ただし\(\lambda > 0\)である．このように正則化項を導入すると，誤差関数を最小化することで同時に\(||\boldsymbol{w}||\)が小さい値に制限される． このような手法を__正則化__という．特に

  • p=1 → Lasso正則化(L1正則化)
  • p=2 → Ridge正則化(L2正則化)

と呼ばれる．L1正則化はパラメータの一部が0に近づくので特徴選択の役割も同時に果たすのだが，解析的に書き下せないためL2正則化が用いられることも多い． \(\lambda\)は正則化の度合を決めるパラメータである．

ちなみに，LassoとRidgeを混合したElasticNetという正則化手法もある．

\[ E(\boldsymbol{w})=\frac{1}{2}||\boldsymbol{y}-\boldsymbol{t}||^2+\lambda\{\alpha||\boldsymbol{w}||+(1-\alpha)||\boldsymbol{w}||^2\} \]

参考

多層パーセプトロンのパラメータの選択については公式のドキュメントが参考になる．

Multilayer Perceptron - DeepLearning 0.1 Documentation

この辺りの機械学習の周辺テクニックについては下記のスライドが参考になる．

機械学習によるデータ分析まわりのお話 from canard0328