最適化とは簡単に言うと関数の最大値・最小値を求めることである． コンピュータサイエンスの応用分野では最適化手法が幅広く用いられている． 機械学習の例で説明すると，例えばデータを学習して”最適な”パラメータを決定するというのは，結局データを引数として取る評価関数を最大化することに他ならない．

しかし，コンピュータで最大値・最小値を計算するのは思ったほど簡単なことではない． 例えば人間なら導関数の零点を見つける際は単純に方程式を解くだけだが，コンピュータに方程式をただ投げても適切なアルゴリズムがなければ解は返ってこない．

この節では，以下の2つのアルゴリズムを説明する．

  1. Lagrangeの未定乗数法

    制約条件付きの最適化問題を解く，数理解析的アルゴリズム． コンピュータが直接的に扱うのは難しいが，様々な最適化アルゴリズムのベースになっている．

  2. 最急降下法

    関数の最大値・最小値を，その導関数を用いて探索的に求めるアルゴリズム． コンピュータにとって扱いやすく，アルゴリズム自体もシンプル（故に問題点も多い）．

Lagrangeの未定乗数法

1変数関数の制約条件付き最大値・最小値を求める際は，導関数の零点から極値をとる値を求め，実際に極値同士の値を比較して最大値・最小値を求めていた．

多変数関数の場合は，

\[ \frac{\partial f(\boldsymbol{a})}{\partial x_1} = 0,\cdots,\frac{\partial f(\boldsymbol{a})}{\partial x_n} = 0 \]

だからといって\(f(\boldsymbol{a})\)が極値になっているとは限らない．

例えば\(f(x,y)=x^2+y^3\)のグラフをプロットすると次のようになる．

臨界点

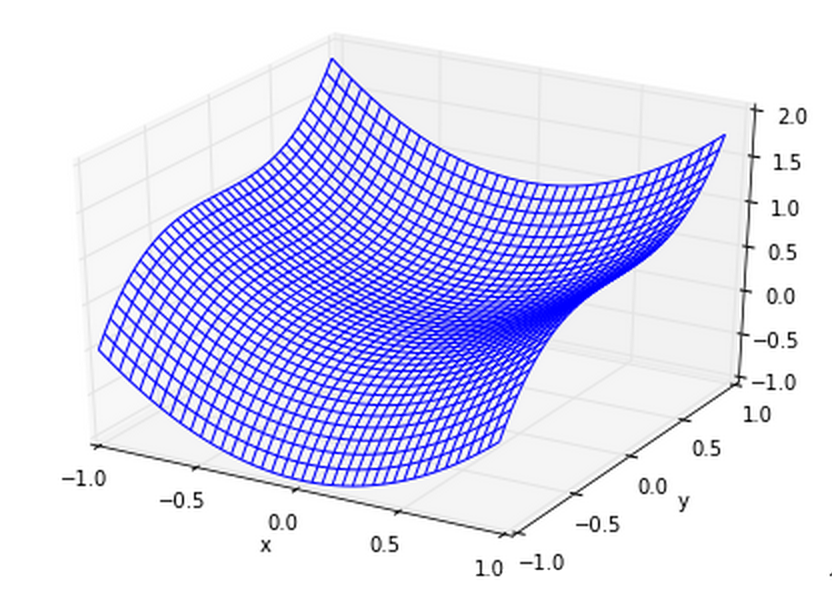
この関数の\((x,y)=(0,0)\)では，\(x,y\)ともに偏導関数は\(0\)になっているが，極値にはなっていない． （極値であるかどうかに関わらず，偏導関数がすべて\(0\)になるような点を停留点，または臨界点という）

1変数の場合でも極値にならない停留点は存在する（例えば\(f(x)=x^3\)の\(x=0\)）が，1変数関数の場合は増減表を書いて確かめることができる． しかし多変数関数では増減表が書けない．ここに制約条件が付いてくると更に複雑になる．

このような多変数関数の制約条件付き最大最小問題を解くにはLagrangeの未定乗数法が用いられる．

Algorithm

制約条件\(g(\boldsymbol{x})=0\)の下で多変数関数\(f(x)\)の極値を与える\(\boldsymbol{x}\)は，次のような関数（Lagrange関数という）

\[ \tilde{f}(\boldsymbol{x},\lambda) = f(\boldsymbol{x})+\lambda g(\boldsymbol{x}) \]

に対して，以下の連立方程式の解として与えられる．

\begin{align} \frac{\partial \tilde{f}}{\partial\boldsymbol{x}} &= 0 \\ \frac{\partial \tilde{f}}{\partial\lambda} &= 0 \end{align}

例1

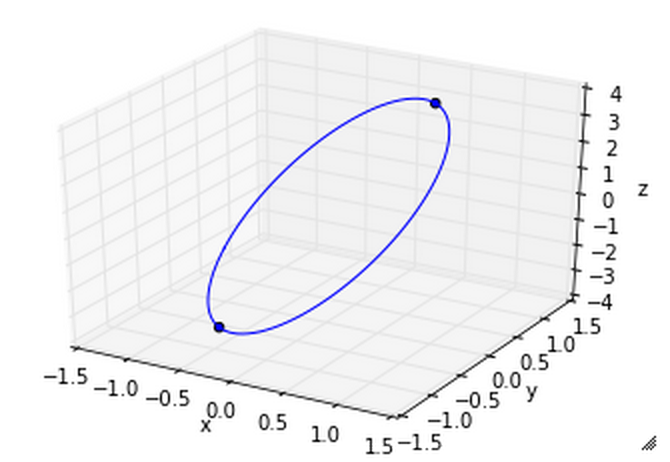
maximize \(f(x,y)=2x+3y\) s.t. \(x^2+y^2=1\)

次のようなLagrange関数を作る．

\[ \tilde{f}(x,y,\lambda)=2x+3y+\lambda(x^2+y^2-1) \]

続いて\(\tilde{f}\)を\(x,y,\lambda\)でそれぞれ偏微分して「=0」とする．

\begin{align} \frac{\partial\tilde{f}}{\partial x} &= 2+2\lambda x = 0 \\ \frac{\partial\tilde{f}}{\partial y} &= 3+2\lambda y = 0 \\ \frac{\partial\tilde{f}}{\partial\lambda} &= x^2+y^2-1 = 0 \\ \end{align}

この方程式から\(\lambda\)を消去すると

\[ (x,y) = (\pm\frac{2}{\sqrt{13}},\pm\frac{3}{\sqrt{13}}) \]

という解が得られる．これらの組は最大値を与える変数の候補になっている． 実際に\(f(x,y)\)に代入してみると，\((x,y)=(\frac{2}{\sqrt{13}},\frac{3}{\sqrt{13}})\)のときに最大値\(\sqrt{13}\)をとり， \((x,y)=(-\frac{2}{\sqrt{13}},-\frac{3}{\sqrt{13}})\)のときに最小値\(-\sqrt{13}\)をとることがわかる．

実際にグラフをプロットしてみると以下のようになる．

未定乗数法の例

練習1

例1のプロットをPythonを使って作成してみよ．

#03やmatplotlibのチュートリアルを参考にするとよい． 3D空間で線を描画するにはAxes3D.plot，点(散布図)を描画するにはAxes3D.scatterを用いる．

（スクリプト例: ex1.py）

練習2

半径1の球に内接する直方体の体積の最大値を求めよ．

解答はex2.mdに示す．

Lagrangeの未定乗数法の原理

厳密な証明は難しく，この分科会の内容から少々逸脱してしまうので，ここでは割愛する． イメージを掴みたい人は，昨年の分科会の資料を参考にするとよい．

複数制約条件の場合

ここでは制約条件が1つの場合のみについて述べたが，制約条件が\(M\)個（\(\{g_m(\boldsymbol{x})=0\}_{m=1}^M\)）ある場合は

\[ \tilde{f}(\boldsymbol{x},\boldsymbol{\lambda}) = f(\boldsymbol{x})+\sum_{m=1}^M\lambda_mg_m(\boldsymbol{x}) \]

というLagrange関数をつくり，以下の連立方程式を解く．

\begin{align} \frac{\partial \tilde{f}}{\partial\boldsymbol{x}} &= 0 \\ \frac{\partial \tilde{f}}{\partial\boldsymbol{\lambda}} &= 0 \end{align}

不等式制約条件の場合

ここで述べたのは制約条件が等式の場合のみであった．制約条件が不等式になっているケースも実用上は多く登場する． その場合は少しだけ複雑になる（Karush-Kuhn-Tucker条件の導入）ので，実際に用いる際に説明する．

最急降下法

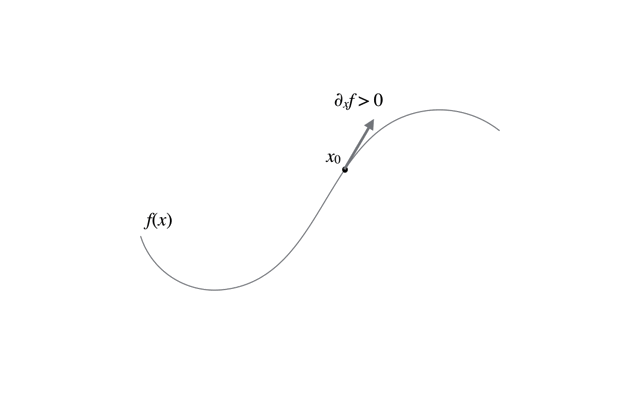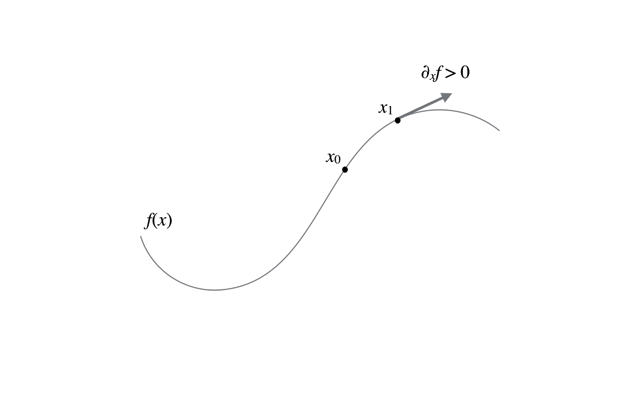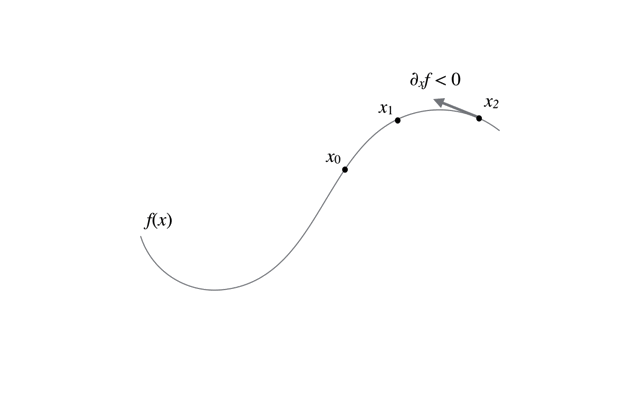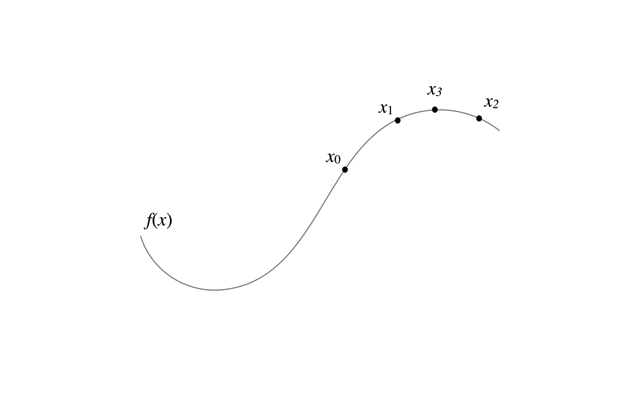
最急降下法は，関数の導関数の値を用いて逐次的に関数値を最大にする解を更新するアルゴリズムである．

関数\(f(\boldsymbol{x})\)に対して初期値\(x_0\)を与えて，

\[ \boldsymbol{x}_{n+1}=\boldsymbol{x}_{n}+\eta\frac{\partial f(\boldsymbol{x}_{n})}{\partial\boldsymbol{x}} \]

で\(\boldsymbol{x}\)の値を逐次的に更新し，収束した点が最大になっている． 導関数の値が0になったら収束だが，実際にちょうど0になる時点まで探索し続けると収束が非常に遅くなるので，導関数値が十分に小さくなったら収束と見なす． イメージとしては，関数値が増大する向き（＝導関数が正）に山を登ることになる．

\(\eta(>)0\)は学習率で，収束の仕方を決めるパラメータである（大きいほど収束が速いわけではない）．

最急降下法の更新の過程の様子は以下のアニメーションを参考にしてほしい．

最急降下法

最急降下法で最小値を求める際は，更新式を以下のように変更すればよい．

\[ \boldsymbol{x}_{n+1}=\boldsymbol{x}_n-\eta\frac{\partial f(\boldsymbol{x}_{n})}{\partial\boldsymbol{x}} \]

最急降下法の問題点

初期値依存性

初期値依存性

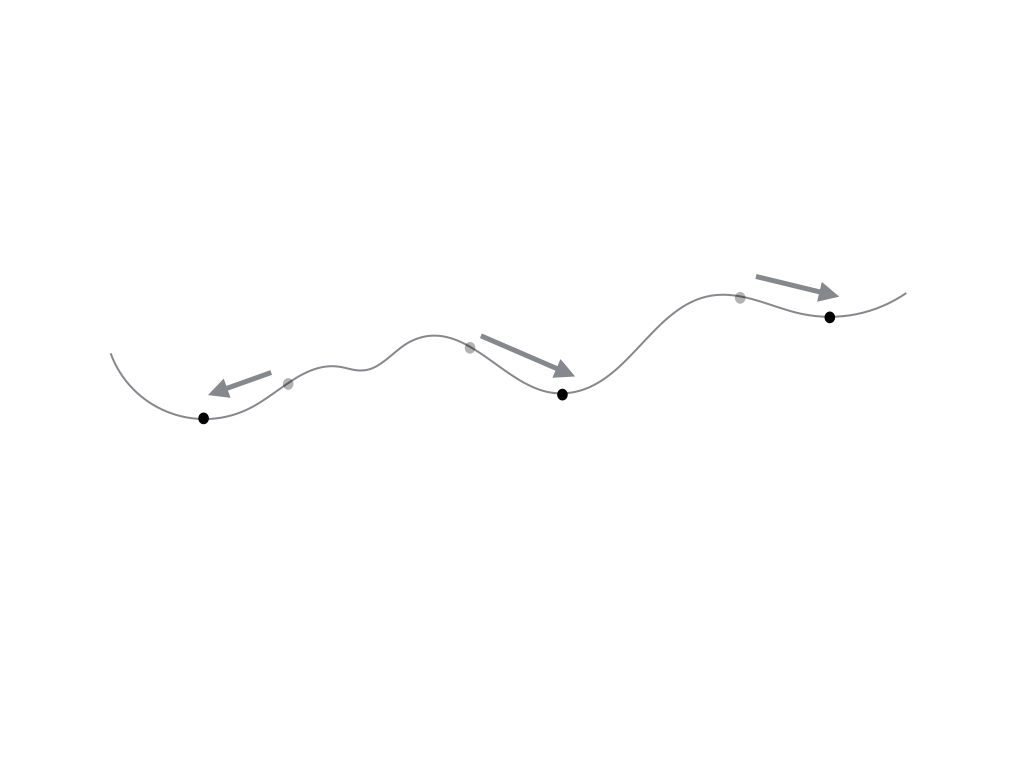
上に示す図のように，最急降下法では初期値の取り方によって収束先が変わり得る． それは，最急降下法は大域的な最大値を求めているのではなく，局所的最大値（すなわち極大値）を求めているからにすぎない． そのため，実際には解析対象となる関数の特性を把握しつつ初期値を選択したり，複数の初期値に対して試行する必要がある．

収束速度

最急降下法は原理がシンプルな反面，収束速度が遅いことで知られる． 学習率\(\eta\)の選び方で収束速度は制御できるが，あまり大きな値にしすぎると見当違いな値に収束することもあり，あまり小さな値にしすぎると収束精度は向上するが収束速度は遅くなるといった問題がある．

例2

#03の例1でプロットした下の関数の最大値を最急降下法で求める．

\[ f(\boldsymbol{x}) = \exp\left(-\frac{(x-0.5)^2+(y-0.2)^2}{2}\right) \]

この関数を微分すると以下のようになる．

\[ \frac{\partial f}{\partial\boldsymbol{x}} = \left(\begin{array}{c} 0.5-x \\ 0.2-y \end{array}\right) f(\boldsymbol{x}) \]

最大値を求めるPythonコードは以下のように書ける．

# coding: utf-8
import numpy as np

# 学習率
eta = 0.1
# 反復回数
N = 200
# 初期値ベクトル
ini = np.array([0, 0])

def f(x):
    return  np.exp(-((x[0]-0.5)**2+(x[1]-0.2)**2)/2)

def f_(x):
    return np.array([0.5-x[0], 0.2-x[1]]) * f(x)

if __name__ == '__main__':
    x = ini
    for i in range(N):
        if i % 10 == 0:
            print("x({}) = {}".format(i, x))
        x = x + eta * f_(x)

ちなみに，このスクリプトのようにコメントにUnicode文字を使いたい場合は，ファイルの先頭に# -*- coding: utf-8 -*-または# coding: utf-8と書く必要がある． この1行によって，Python処理系はUTF-8でスクリプトを解釈するようになる．

練習3

例2のスクリプトを実際に動かしてみよ．また，学習率，反復回数，初期値ベクトルを変化させると収束先の値がどのように変化するか，いろいろ試してみよ．

練習4

例2で，収束するまでの反復回数が最も少なくなるような学習率を探索せよ．0から2の間で試せば十分である．

ex4.pyにスクリプト例を示す．